The information below describes and shows how the area of any two dimensional surface may be calculated simply and swiftly by use of a Digital Camera and a simple software program designed and developed by the author.

The area of simple two dimensional shapes having known dimensions and the area of irregular shapes having known perimeters are easily calculated. However, when the dimensions or perimeter are not known, calculating the area of a two dimensional surface may be difficult and time consuming.

The photo below shows an object having an irregular surface for which the viewed surface area needs to be calculated:

This area may be calculated by taking a photograph of the object and then executing a simple software program. The procedure is described in the steps below. Note that the second step will be unnecessary in a future upgrade to the software program.

Step 1: Photograph Object

Photograph the object against a background having known dimensions and that has a color that is highly contrasted with the color of the object. The photo below is of the dark colored object on the back side of a white 3" wide by 2" high business card on a sheet of black paper:

Step 2: Select Background Area In Image File And Save To 16 Color Bit Map File

Load the photograph image file produced by the Digital Camera into Microsoft Paint. Select the background of known dimensions and click on "Edit" and then "Copy". Acquire the selected area by clicking on "File" followed by "New" and then "Edit" followed by "Paste". Write the acquired image to a 16 Color Bitmap file by clicking on "File" followed by "Save As..." and then select "16 Color Bitmap" in the "Save as type:" option. The image below is of the example above:

Step 3: Execute Software Program To Determine Area

Execute the software program with the image file created. The program displays the image and also generates the results given below:

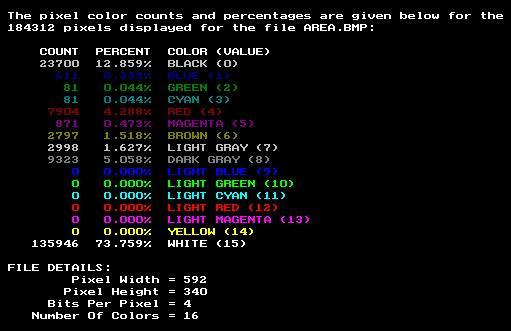
The results given above indicate that 73.759 percent of the image consists of white colored pixels. The white colored pixels are those that represent the exposed white background in the image. The remaining 26.241 percent (100 - 73.759 = 26.241) of the background area is consumed by the object area. Since we know the total background area is 6" square (3" X 2" = 6" square) and 26.241 percent of this area is that of the object, the area of the object is 1.57446" square.
That is: 6" square X 0.26241 = 1.57446" square

The image created is given again below for convenience:

Note, however, that the light gray colored pixels in the image represent shadows cast by the object onto the background. Since the area of these shadows is that of the exposed background, the exposed background actually consists of the white pixels as well as the light gray pixels. Therefore, the exposed background is actually 75.386 percent (73.759 + 1.627 = 75.386) of the image. Thus, the area of the object is actually 1.47684" square.
That is: 6" square X (1 - 0.75386) = 1.47684" square